Ruijie Fu

I am a graduate student at the CMU Biorobotics Lab. From 2016 to 2020, I studied at Carnegie Mellon University as a math major undergrad. I had a minor in robotics at Robotics Institute, part of the School of Computer Science, where I work on geometric mechanics and SLAM. My research advisor is Howie Choset.

I'm interested in differential geometry, bio-inspired robot locomotion, robot localization and mapping, and computer graphics. My recent work has been on geometric mechanics and sequence matching.

Email  /  Resume

Research

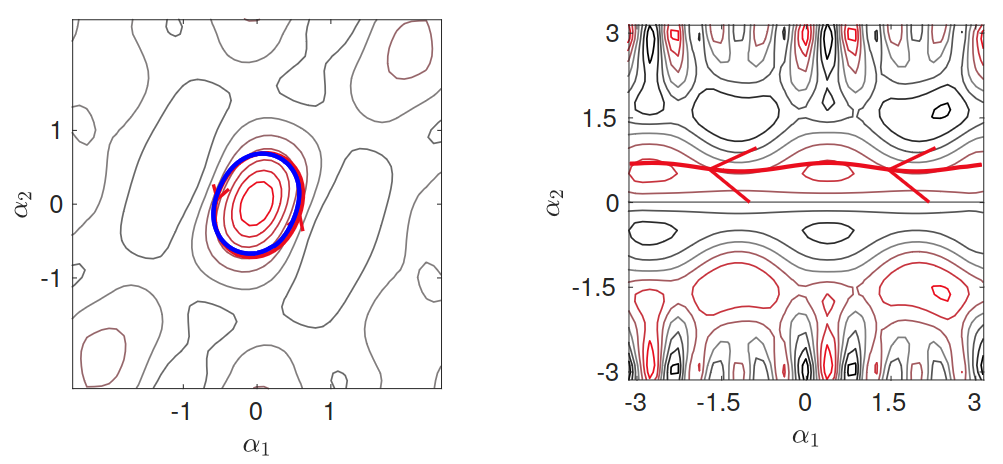
Towards Mechanical Communication in Multi-Agent Locomotive Systems

Many biological multi-agent systems exhibit a mechanism for information exchange among individuals known as mechanical communication, which leads to the emergence of collective behavior within the group. Similarly, multi-agent groups of articulated robots in a shared environment can dynamically adjust their shape and movements, influencing each other’s motion through the ambient media. Recognizing the potential significance of this mechanism, we would like to investigate and harness the power of mechanical communication in the control of multi-agent locomotive systems.

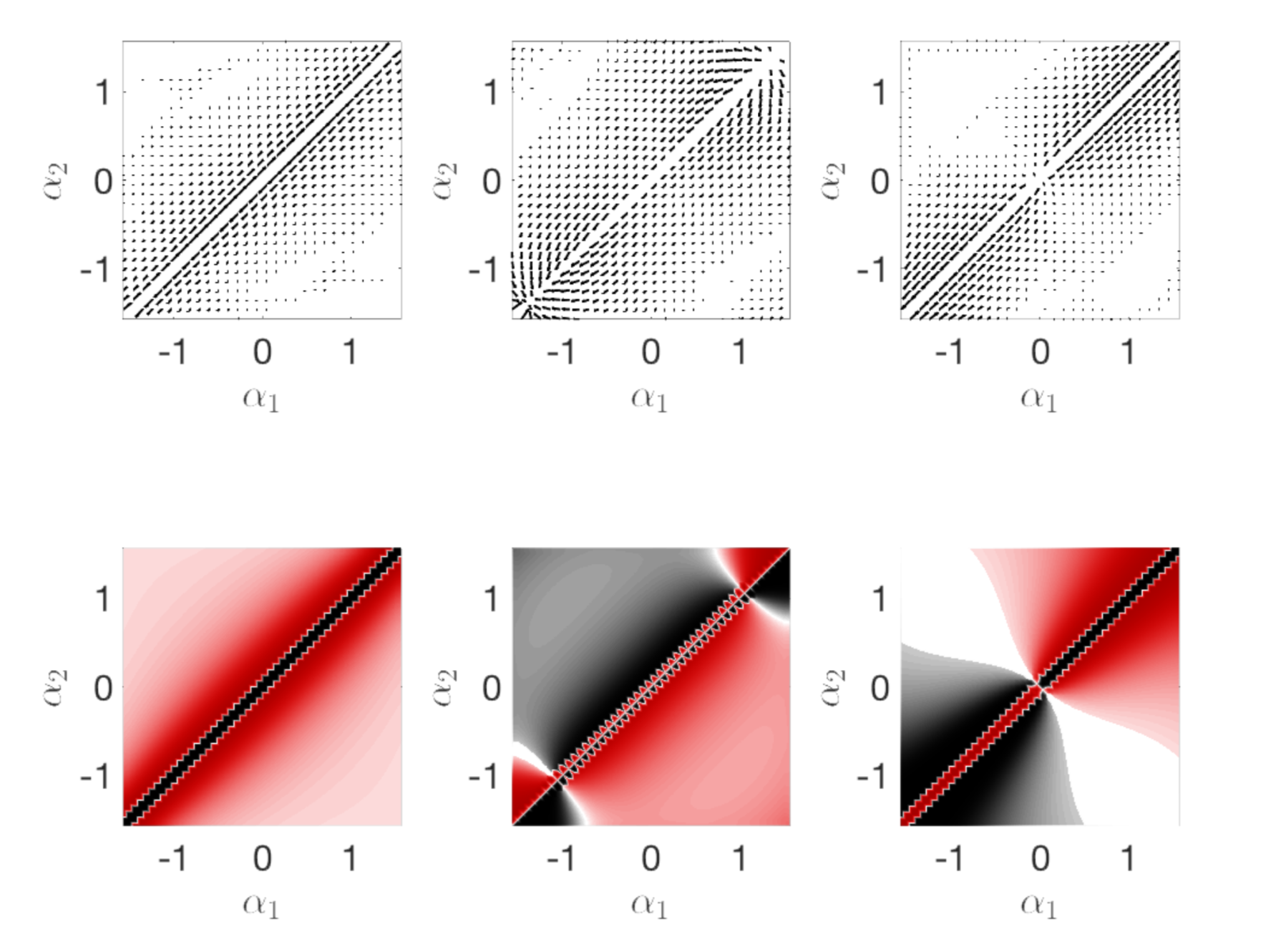
Geometric Motion Planning for Systems with Cyclic Shape Spaces

Previous research in geometric mechanics has primarily focused on shape spaces that do not include cyclic internal degrees of freedom, such as revolute joints without joint limits. This work extends prior work to cyclic shape spaces, including shape spaces that are cylinders and tori. By explicitly analyzing the topology of the underlying shape space, we consider simple closed paths that wrap around the cyclic degree of freedom and derive geometric tools for motion planning and gait optimization on cyclic shape spaces.

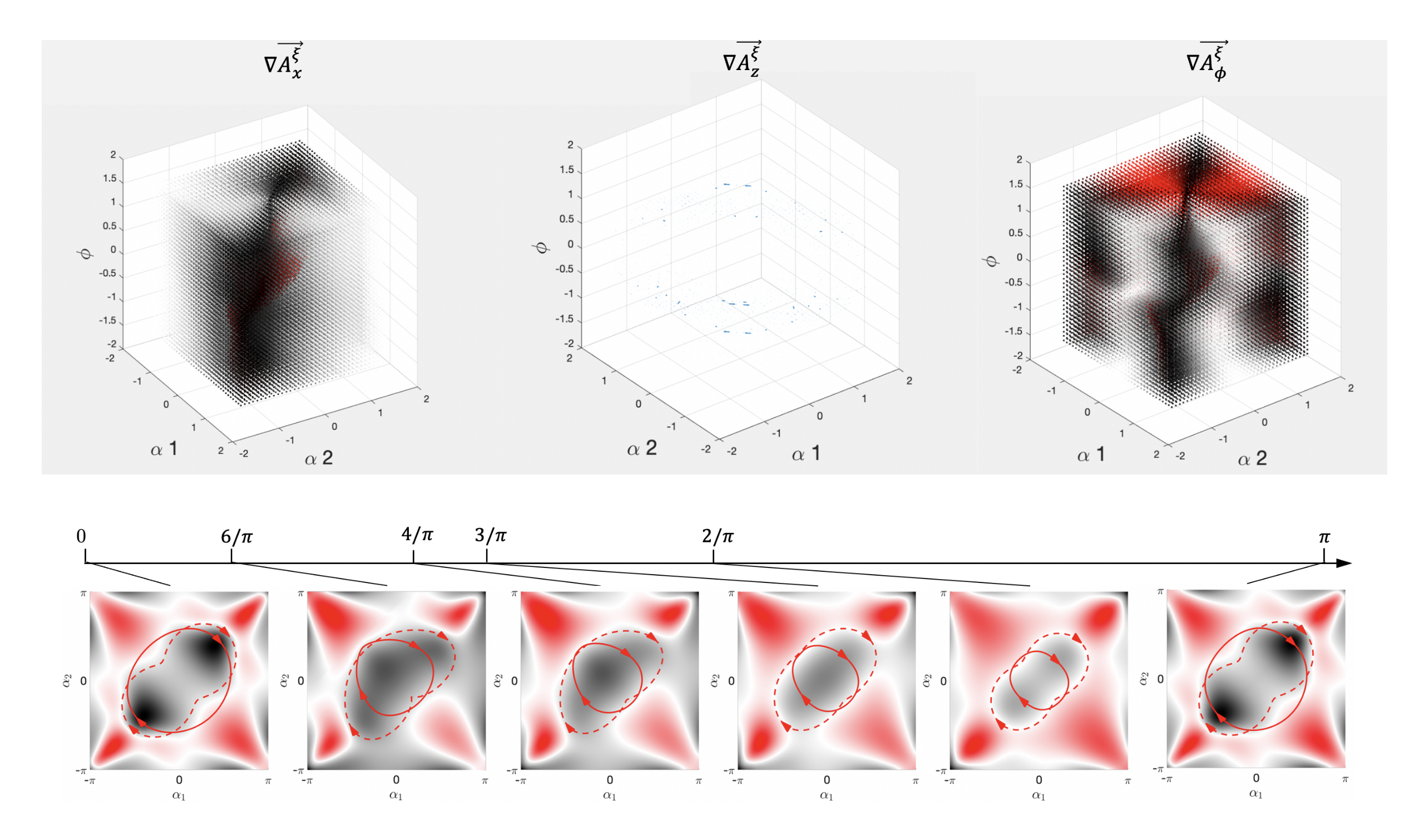
Motion Planning for Kinematic Snake under singular configuration

Kinematic snake runs into singular configurations when the nonholonomic constraints are violated (e.g. one or more of the constraint equations becomes a linear combination of the others), at which point the matrix inverse becomes analytically unsolvable and thus causing discontinuities. We propose an optimization algorithm for finding high-efficient gait of nonholonomic kinematic snake that purposely enclose the singularity region, which ultimately produces the best gaits given specified input energy cost functions. Refer to the back ground paper linked above for the application of geometric mechanics to studying robot locomotion.

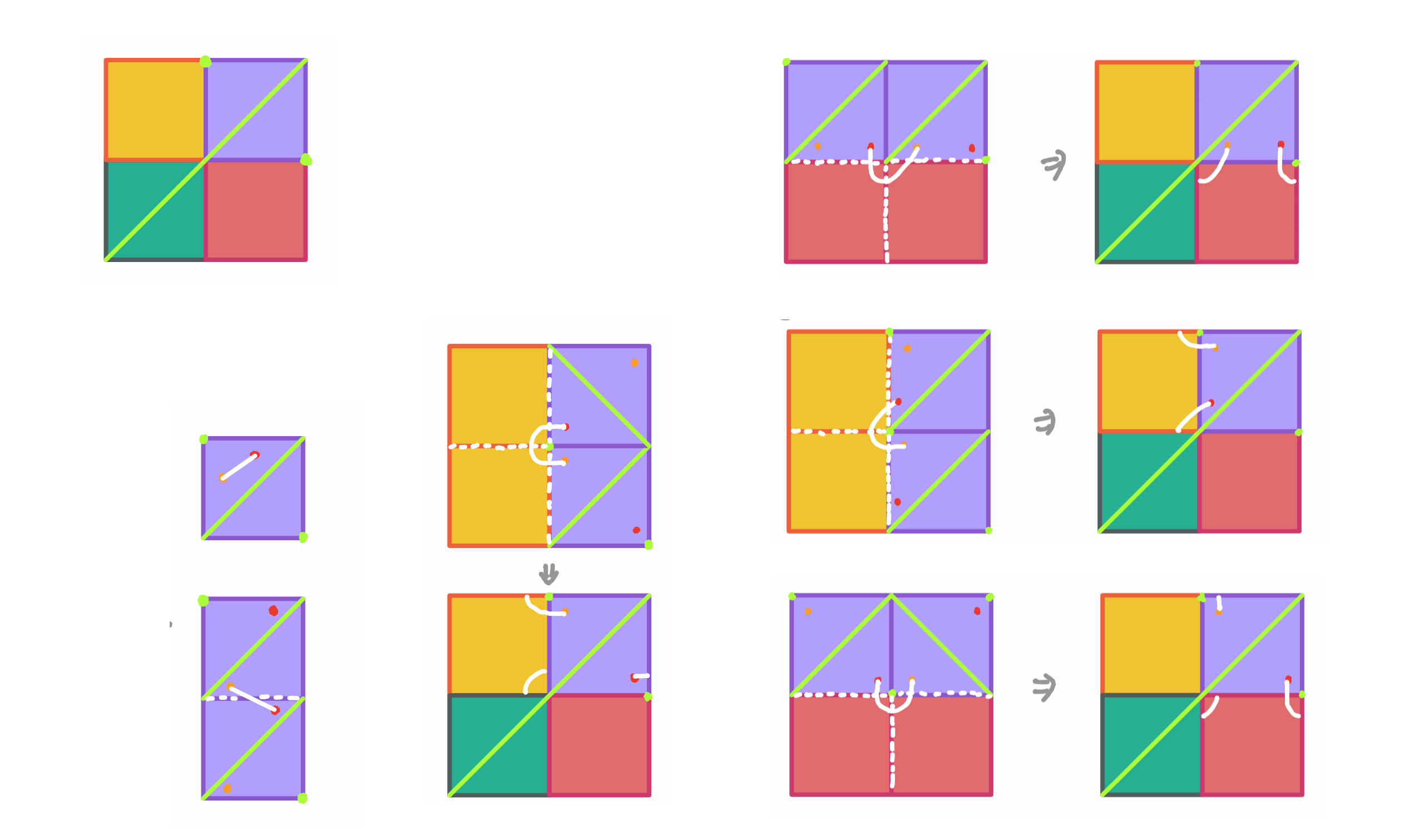
Geometric Motion Planning for Systems on Cylindrical Surfaces

This work studied a newly designed three-link, quasi-static system operating on curved surface. This new model allowed us to explore to what extent the traditional geometric concepts, such as the local connection and the lie bracket techniques, can be used in motion planning on curved position space. We introduced a new “constraint projection” method to a variational gait optimizer and demonstrated how to design gaits that allow this example system to move on an inner cylindrical wall.

Geodesic Complexity of Motion Planning on Lollipop Graph

Similar to the definition of topological complexity, geodesic complexity is a property that encodes the minimum number of continuous path planning rules needed to describe the geodesic between robot system’s starting configuration and ending configuration in a space. It is invariant under isometries. We find a metric space that potentially has higher geodesic complexity than topological complexity, and study it by using the stratification method as given in the background paper above.

Project

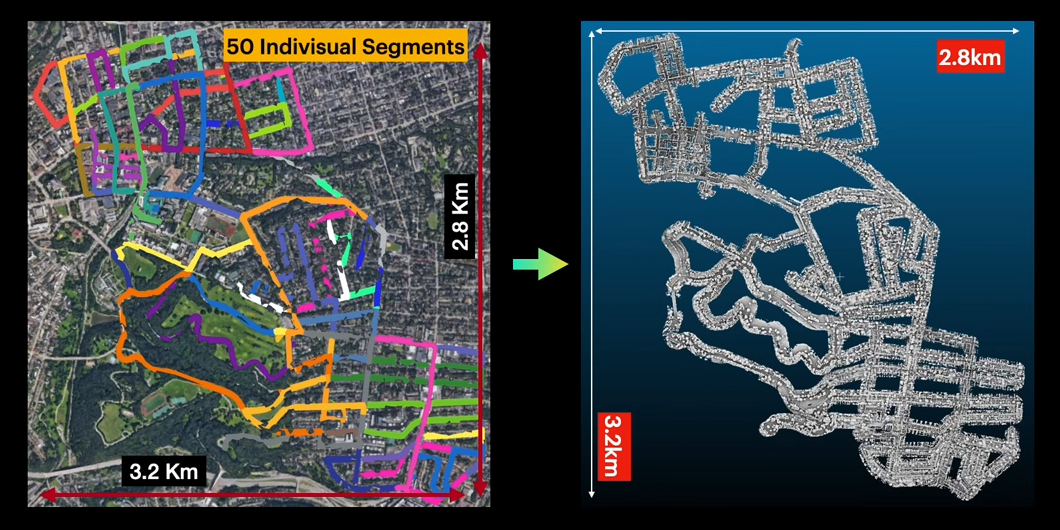
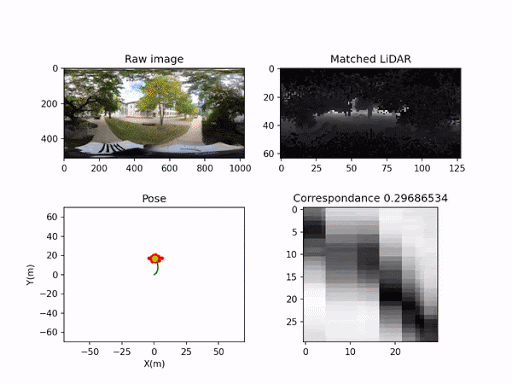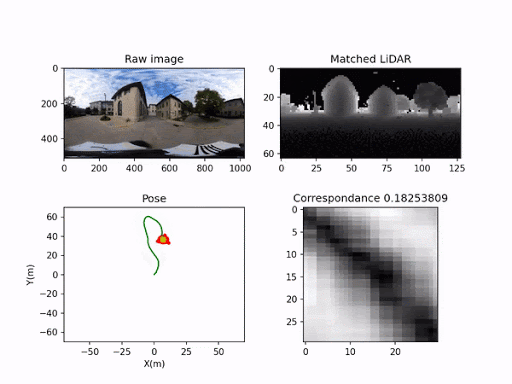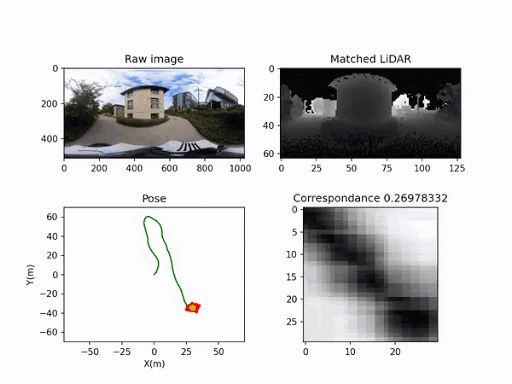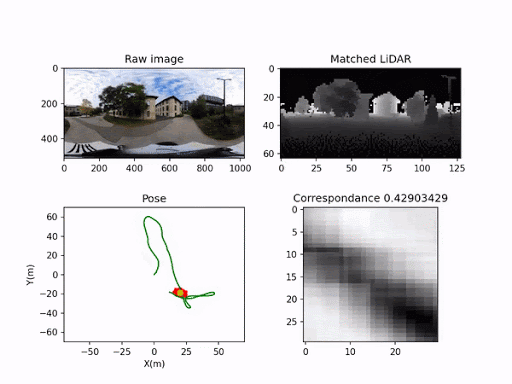
AutoMerge: A Framework for Map Assembling and Smoothing in City-scale Environments

Automerge is an efficient LiDAR data processing framework that quickly and accurately assembles large numbers of map segments into a complete map, enabling autonomous mobile robots to communicate and coordinate their movements. I was mainly in charge of enhancing the performance of sequence matching and testing the spherical convolutional LiDAR features.

Localizing a Monocular Camera in a 3D Point Cloud Map

Our aim is to map once with UGV equipped with lidar, and reuse the lidar map multiple times for resource-limited UAVs with only onboard cameras. To achieve this goal, we utilize an original spherical convolution feature that is invariant to the orientation, and the sequence matching algorithm extended to 2d.

Iris Lunar Rover

Iris is an ultra light weight lunar rover designed by CMU students. It will land on the moon in the fall of 2021. I was in charge of designing the ground operation code translation chart, building up modules and coding for flight software, as well as designing the teleoperation software structure.

Design and source code from Leonid Keselman's website